Teoria dei campi

La Teoria Quantistica dei Campi (QFT) è lo strumento base per descrivere il comportamento delle particelle elementari e le interazioni fondamentali. Al momento abbiamo un ottimo controllo della QFT a livello perturbativo mentre una piena comprensione degli aspetti non-perturbativi è attualmente oggetto di ricerca. Le principali linee di ricerca comprendono:

Geometria e topologia: modelli sigma non-lineari; quantizzazione di Batalin-Vilkovisky nella formulazione geometrica di Alexandrov-Kontsevich-Schwartz-Zaboronsky; teoria di gauge superiore.

Metodi linea-di-mondo: metodi di prima quantizzazione, ispirati dalla teoria delle stringhe, per studiare ampiezze di scattering e azioni effettive in teorie di gauge e gravità.

Anomalie: proprietà e implicazioni fisiche delle anomalie quantistiche chirali e di traccia.

Gruppo di rinormalizzazione: studio di QFT con metodi perturbativi e non-perturbativi in dimensioni arbitrarie; gruppo di rinormalizzazione funzionale, perturbativo o Wilsoniano, per determinare proprietà universali, simmetrie e rinormalizzabilità di teorie invarianti di scala o conformi; azioni effettive e matrice S.

Integrabilità: calcolo esatto di quantità fisiche tramite integrabilità quantistica con applicazioni in fisica del non-equilibrio, entanglement, catene di spin, gruppo di rinormalizzazione in QFT 2D, così come in teorie di gauge 4D N=2 supersimmetriche per implicazioni fenomenologiche e in corrispondenza con perturbazioni di soluzioni gravitazionali, buchi neri e onde gravitazionali.

Attività

Aspetti geometrici e topologici della teoria dei campi e delle stringhe

Modelli sigma non lineari.  Quantizzazione  di Batalin-Vilkovisky nella formulazione geometrica di Alexandrov-Kontsevich-Schwartz-Zaboronsky. Teoria di gauge superiore.

Metodi Worldline

Studio di metodi di prima quantizzazione, noti come “worldline methods”. Lo scopo è quello di trovare rappresentazioni alternative di ampiezze di scattering e azioni efficaci in QFT con accoppiamenti di gauge e gravitazionali, anche ispirandosi alle teorie di stringhe.

Anomalie in QFT

Le anomalie descrivono la rottura quantistica di simmetrie classiche. Hanno applicazioni di vasta portata, che vanno dal vincolare il contenuto di materia delle teorie di gauge alla caratterizzazione di proprietà non perturbative delle QFT e del loro comportamento sotto l'azione del gruppo di rinormalizzazione.

QFT, CFT in d>2 e gruppo di rinormalizzazione

Lo spazio astratto delle possibili teorie quantistiche di campo è caratterizzato da punti invarianti rispetto a trasformazioni di scala (punti fissi del gruppo di rinormalizzazione) o conformi. Considerando le simmetrie che il contenuto di spin determina, si formulano nuove teorie di campo complete nell’UV e si studiano nuove classi di universalità in teorie statistiche e nella costruzione di nuovi modelli di interazioni fondamentali oltre quello standard

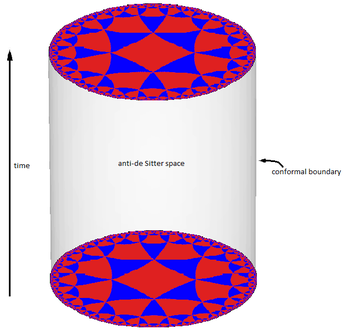
Integrabilità in teorie supersimmetriche in 4D, stringhe e metodi di Bethe ansatz

L’integrabilità è una proprietà profonda di una classe di teorie che permette di calcolare esattamente quantità fisiche non banali grazie ad una struttura fisica e matematica soggiacente. In generale, tale proprietà si manifesta in maniera naturale in due dimensioni e se appare in dimensioni più elevate diventa ancora più rimarchevole.  Il nostro interesse si concentra sulle teorie di gauge supersimmetriche in 4D, che rivestono anche un interesse fenomenologico, e sul loro legame (dualità) con  teorie di stringa, dove la struttura bidimensionale della teoria porta naturalmente all’integrabilità. Lo scopo finale di questi studi è quello di arrivare a modelli più fondamentali e realistici per le interazioni. Nelle teorie di campo integrabili è possibile considerare, in maniera esatta e unificata, il problema del comportamento termodinamico e quello degli effetti di volume finito, usando l’idea del Bethe Ansatz Termodinamico (TBA). Lo sviluppo delle strutture matematiche soggiacenti al TBA ha rivelato architetture algebriche e analitiche sorprendenti, connesse con altri ambiti della matematica e della fisica e tuttora oggetto di attivi e coinvolgenti approfondimenti.

Fisica del non equilibrio e campi quantistici

La fisica del non equilibrio è una delle maggiori sfide della meccanica statistica moderna. Gli sviluppi degli ultimi anni hanno enfatizzato l’esistenza di metodi di QFT per affrontare questi fenomeni, non solo a livello classico, ma anche a quello quantistico, ove sono collegati alla fisica degli atomi freddi e dei condensati bosonici. L’approccio a “quantum quench” è ormai maturo, mentre la idrodinamica generalizzata (GHD) è in una fase di attivo sviluppo in questi ultimi anni. In entrambi gli approcci, l’integrabilità e la fisica non perturbativa giocano un ruolo essenziale.

Compattificazioni di stringa

Studio della teoria effettiva di supergravità in quattro dimensioni per compattificazioni di stringa su spazi di Calabi-Yau con brane, orientifold e flussi di background. Calcolo di correzioni perturbative e non-perturbative. Stabilizzazione dei moduli di stringa aperta e chiusa. Meccanismi di rottura della supersimmetria e realizzazione di vuoti di de Sitter in modelli di D-brane chirali che sono globalmente consistenti e danno luogo a promettenti applicazioni alla cosmologia ed alla fisica delle particelle.

Teoria dei campi in spazi curvi

Sviluppo di metodi della teoria dei campi quantistici in spazi curvi, soprattutto del gruppo di rinormalizzazione, per applicazioni ai problemi di gravità quantistica e cosmologia.

Progetti e collaborazioni nazionali e internazionali

Le attività di ricerca in questa linea si inquadrano anche nell’ INFN, ST&FI, GAST, FLAG. Numerose collaborazioni sono attive con Università/Istituti italiani (Modena, Trieste, Roma, Padova) e stranieri [Morelia (MX), Potsdam (DE), Cambridge (UK), Oxford (UK), Durham (UK), King’s College (UK), City University (UK), DESY (DE), Heidelberg (DE), Perimeter (CA), Texas A&M (US), Colorado (US), Oklahoma (US), New Mexico (US), HRI Institute (IN), Ewha University (KR), Paris (FR), Melbourne (AU), Budapest (HU) ] .